Ball valve shrinkage coefficient and flow coefficient

1. Introduction

Due to its good sealing, no hysteresis, high working pressure, insensitivity to pollution, simple manufacture, and few failures, ball valves have recently been favored by people and are widely used in various hydraulic systems.

As far as the performance evaluation index of the ball valve is concerned, the pressure and flow characteristic is undoubtedly an important index to measure its working characteristics. The relationship between the outlet flow of the ball valve and the pressure difference between the inlet and outlet can be characterized by the following formula:

In the formula: C——flow coefficient; Ax——valve port flow area; △P——valve inlet and outlet pressure difference; ρ——fluid density.

It can be seen from equation (1) that the relationship between Q and △P depends on C and A when the flowing medium is determined. A can be determined by the geometric characteristics of the valve structure. C is a very complex quantity, which is related to the fluid flow state, the geometric structure of the valve and other factors. Its determination mostly depends on experimental methods. At present, there is no theoretical calculation formula and general empirical or semi-empirical formula for calculating the flow coefficient of the ball valve, which brings great inconvenience to the design and application of the ball valve. In order to fill this gap, starting from the flow mechanism of liquid flow, it is particularly important to propose a simplified model for calculating the flow coefficient of the ball valve.

2 Determination of flow coefficient

The size of the flow coefficient actually reflects the comprehensive influence of the loss of resistance when the orifice flows out and the reduction of the overcurrent interruption on the outflow flow rate, which can be expressed by the following formula:

In the formula: φ——fluid outflow velocity coefficient; μ——shrinkage coefficient.

(1) Calculation of velocity coefficient

According to the document "Fluid Mechanics and Fluid Machinery", the following formula can be obtained:

In the formula: ξ-local resistance coefficient

Figure 1 Ball valve structure

For the situation in Figure 1, according to the document "Machine Design Manual (Volume IV)":

In the formula: A——Entrance cross-sectional area

Their calculation formula is as follows:

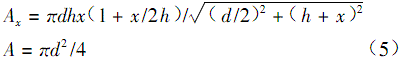
In the formula: d——the diameter of the valve seat hole; x——the lift of the valve core; R——the diameter of the steel ball.

Therefore, the flow rate coefficient can be calculated as follows:

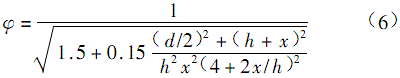
Simplified calculation model of shrinkage coefficient μ

As shown in Figure 1, the liquid flow flows out through the gap between the valve seat and the steel ball. According to the theory of the boundary layer, it is impossible to separate the outflow on the hemispherical surface in front of the steel ball, but separation may occur at point A of the valve seat. Or the streamline changes its direction to cause the flow section to shrink. From this mechanism, the flow through the gap of the valve port can be divided into two parts, one part flows along the aisle wall, and the other part flows along the steel ball wall. The fluid flowing along the wall of the aisle has sharp corners due to the change of the wall shape, which causes a sudden change in the direction of the streamline. The flow cross section shrinks on the edge of the valve seat, while the flow along the side of the steel ball does not shrink. . Therefore, the flow between the steel ball and the valve seat is actually an annular flow that shrinks on the outside and does not shrink on the inside. Since the annular gap flow gap is relatively small, according to the gap flow theory, it can be expanded into a gap flow between two flat plates. Furthermore, due to the shrinkage of the outer side, it can be simplified into the outflow flow model of the bottomless sluice hole as shown in Figure 2, and the corresponding size is shown in Figure

Figure 2 Simplified model of liquid flow in ball valve

The outer shrinkage coefficient of the annular flow can be calculated and selected according to the outflow condition of the gate hole.

The sluice flow shrinkage coefficient μ can be evaluated by the analysis method of Jukovsky theory, as shown in Table 1.

Therefore, the flow coefficient C can be calculated according to formula (5) and Table 1.

Table 1 The shrinkage coefficient μ value corresponding to the model

3 Experimental research

Strictly speaking, the ball valve flow coefficient C is closely related to the Reynolds number Re (Re=Q/4dv), and the change of C with Re can be written as the following relationship:

In the formula: K and n are coefficients and exponents, which are related to the shape of the valve structure.

Studies have shown that Re has a critical value Rec, and Re increases with the increase of the ratio d/(2R). When Re exceeds Rec, C does not change with Re, but tends to be constant. Generally speaking, Rec is often very small, and Rec is much larger than Rec when the ball valve is working normally. Therefore, it can be considered that under working conditions, C is a constant.

In order to verify the validity of the model and the relationship between Rec and valve geometry, we conducted experimental research on ball valves with different geometric parameters and found that after Re is greater than Rec, the calculation results of the model are in good agreement with the experimental results.

4 Conclusion

(1) The flow coefficient of the ball valve varies with Re in a small range. Re has a critical value Rec. When Re>Rec, C tends to be constant

(2) When Re>Rec, the calculation result of the wood model is in good agreement with the experimental value, so this model can be used to calculate the ball valve flow coefficient.